Skip to main content

Union Find

The Two Useful Operations​

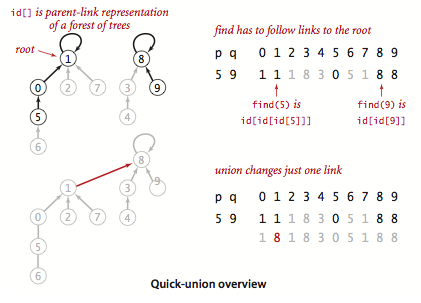
  • Find Operation: O(N)
    • Used to find which component a particular element belongs to
    • Find the root of the component by following the parent nodes until a self loop is reached(a node who's parent is itself)
      • On the picture you can see [8 is paired with 8], [1 is paired with 1]
def find(x):
	if Parent[x] != x:  #not self-loop
		return find(Parent[x])
	return x
  • Union Operation: O(N)
    • Used to unify two elements
    • Find which are the root nodes of each component and if the root nodes are different make one of the root nodes be the parent of the other.
def union(x,y):
	root_x, root_y = find(x), find(y):
	if root_x != root_y:
		Parent[find(y)] = find(x)
#Example check whether or not the elments x and y are in the same components
def connected(x,y):
	return find(x) == find(y)

Optimizing Find Operation: Union Find Path Compression​

The previous operation on worst case performs O(n) since we will need to hop n times to reach the root.

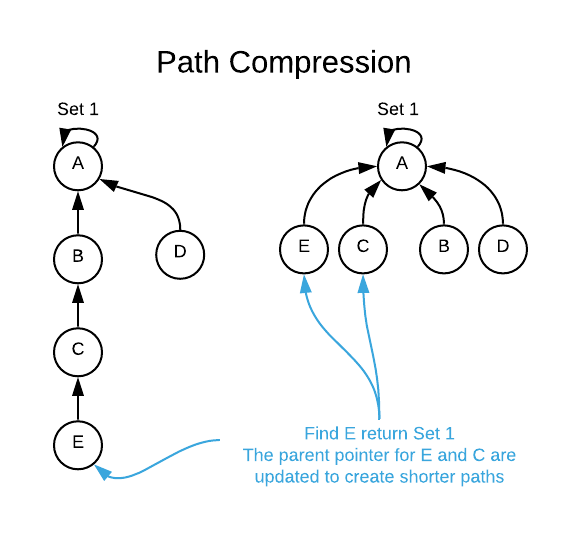
  • Path compression
    • The idea is to flatten the tree when find() is called.
    • Path compression is to make the found root as parent of x so that we don’t have to traverse all intermediate nodes again.
    • If x is root of a subtree, then path (to root) from all nodes under x also compresses.
def find(x):
	root = x
	while Parent[root] != root:
		root = Parent[root]

	while x != root:
		Parent[x], x = root, Parent[x]
	return root

# or with recusion
def find(x):
	if self.par[x] != x:
		self.par[x] = self.find(self.par[x])
	return self.par[x]

Optimizing Union Operation: Union by Rank​

  • Union by rank optimizes the union operation in Union-Find.
    • It ensures the tree with fewer nodes is attached to the root of the tree with more nodes.
    • This optimization aims to keep the overall height of the tree minimal.
    • It improves the efficiency of both union and find operations.
    • The rank of a tree serves as an upper bound on its height.
    • During union, the tree with lower rank is attached to the root of the tree with higher rank.
    • This prevents the tree from becoming unbalanced, maintaining performance.
    • Union by rank helps reduce the worst-case time complexity of find operations to nearly constant time.
    • Overall, it enhances the efficiency and effectiveness of the Union-Find data structure.
  • union by rank

Template for Union Find​

class UF:
    def __init__(self, n):
        self.par = {i:i for i in range(n)}
        self.rank = [1] * n
    
    def find(self, x):
        if self.par[x] != x:
            self.par[x] = self.find(self.par[x]) #path compression
        return self.par[x]
    
    def union(self, x, y):
        px, py = self.find(x), self.find(y)
        if px == py:
            return

		# union by rank
        if self.rank[px] < self.rank[py]:
            self.par[px] = py
            self.rank[py] += self.rank[px]
        else:
            self.par[py] = px
            self.rank[px] += self.rank[py]

	# additional: optional functions
	def connected(self, x, y):
		return self.find(x) == self.find(y)

Application of Union Find​